
实验四 贪心算法
问题描述
一.实验目的
掌握贪心算法的设计与分析步骤以及算法的具体实现。
二.实验要求
实验时间:2学时,对于给定的问题描述,生成实验报告。
三.实验内容
问题描述:设有$n$种零钱, 重量分别为$w_{1},w_{2},\dots,w_{n}$,价值分别为$1, v_{2},\dots,v_{n}$, 其中$v_{1} < v_{2} < \dots < v_{n}$ 需要付的总钱数是$Y$。假设币值和钱数都为正整数。问:如何付钱使所付钱的总重最轻?
- 使用动态规划算法解决问题,给出分析过程。
- 使用贪心算法解决问题,给出分析过程。
- 给出算法的具体实现过程(源码及其详细注释)。
- 给出算法的运行结果。针对不同的输入,分析贪心法和动态规划法得到的解是否相同,如果不同,给出理由。
形式化问题
现有集合 $W={w_{1},w_{2},\dots,w_{n}}, V={v_{1}, v_{2},\dots,v_{n}}$ ,且满足 $v_{1} < v_{2} < \dots < v_{n}$ .对于给定的 $Y$ ,找出合适的 $X={x_{1},x_{2},\dots,x_{n}}\space,x_{i}\in n$ ,满足 $Y=\sum_{i=1}^{n}v_{i}x_{i}$ ,求满足条件的 $X$ 中,同时满足 $min{\sum_{i=1}^{n}w_{i}x_{i}}$ 的集合结果.
动态规划算法
这属于整数规划问题,动态规划算法可以得到最优解。
解决DP问题,最重要的是要找出子问题。所以从这里开始。
此问题基于初始的硬币问题,下面给出题面
假设有 1 元,3 元,5 元的硬币若干(无限),现在需要凑出 11 元,问如何组合才能使硬币的数量最少?
初始的硬币问题相当于此问题中的特例,要解决题目中的问题,不妨先从这个特例开始:
特例
现在给定一个$W={1,1,1}$ , $V={1,5,10}$ , $Y=15$ ,求 $X$ 的 $min{\sum_{i=1}^{n}w_{i}x_{i}}$ (注意,这里求的是最小个数sum,而不是支付方式$X$).
在这里我们将硬币看做等重量,即1,此处映射为对应面额硬币的个数。
我们给定一个二维数组F[k][y],表示当前考虑 $1,2,\dots,k$ 的情况下,对于当前金额 $y$ 所需的最小重量(硬币数)。
我们从头开始,很显然,对于F[1][],即只考虑 1 元硬币的情况,对于给定的当前 v 的最小值。
将 $v=0$ 置为0.接下来考虑要付 1 元钱的情况,这时只可能有 在原先0元的基础上付 1 元硬币。即 $F[1][1]=F[1][0]+w_{1}x_{1}$.
| 金额 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| F[1][] | 0 | 1 | 2 |
以此类推,直到 $y=Y$.
| 金额 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| F[1][] | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
接下来我们考虑 $k=2$ ,即有1元和5元硬币的情况。在 $y < 5$ 的情况下,不能用5元硬币,所以此时直接等于其上面的值。
直到 $n=5$ 可以看到此时可以拿一个5元的硬币了。我们直接从 F[2][0],F[1][5] 中查找最小值,然后加上5元的重量1.
提示
有人还会考虑了
F[1][0]的情况,但事实上, 由于最优子结构的性质,在考虑F[2][0]时已经考虑过F[1][0],所以不用再考虑,以此类推,在考虑n=6时,F[0][1]不用考虑,等等等等
继续分析
| 金额 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| F[1][] | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| F[2][] | 0 | 1 | 2 | 3 | 4 | 1 |
同样,对于10元,15元也是同样的处理方法。
| 金额 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| F[1][] | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| F[2][] | 0 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 5 | 2 | 3 | 4 | 5 | 6 | 3 |
以此类推,填完表格
| 金额 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| F[1][] | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| F[2][] | 0 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 5 | 2 | 3 | 4 | 5 | 6 | 3 |
| F[3][] | 0 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | 2 |
状态转移方程
设 $F_{k}(y)$ 表示用前 $k$ 种零钱,总钱数为 $y$ 的最小重量。
$$\left{
\begin{matrix}F_{k+1}(y)=\min
\begin{Bmatrix}F_{k}(y)
\F_{k+1}(y-v_{k+1})+w_{k+1}
\end{Bmatrix}
\F_{1}(0)=0
\end{matrix}\right.$$
$$k=1,2,\dots,n-1,y=0,1,\dots,Y$$
PPT上给出了另一种状态转移方程,但我倾向于用上方的二选一的方式表达。
下面是PPT给出的状态转移方程。
$$\left{\begin{matrix}f_{k+1}(y)=\min_{0 \le x_{k+1} \le \left \lfloor \frac{y}{v_{k+1}} \right \rfloor }{F_{k}(y-v_{k+1}x_{k+1})+w_{k+1}x_{k+1}}
\f_{1}(y)=w_{1}\left \lfloor \frac{y}{v_{1}} \right \rfloor =w_{1}y
\end{matrix}\right.$$
$$k=1,2,\dots,n-1,y=0,1,\dots,Y$$
复杂度
此算法常数级填写了一张二维表格。时间复杂度为
$$O(nY)$$
$n$ 为钱的种数,$Y$ 为需要给付的钱数。
若需要具体的$X$集合,只需同样[n][Y]大小的数组(或者一个[2][Y]的数组进行滚动),用来存取其选择的单元格,然后通过 $O(n+Y)$ 回溯计可获得 $X$ 的集合。
贪心算法
用贪心算法解决此问题,只需要保证每次选择都是当前最好的选择。
针对当前问题,为了能够得到最小的总重量
我们就会优先选择单位重量下价值较高的硬币。直到不能再用,再选单位价值次之的。由于题干说明一定有价值为1的硬币,所以一定能保证付到Y价值。
复杂度
此算法需要将硬币按“单位价值比”排序,最快需要 $O(n \log n)$ 时间,此后选择只需要 $O(n)$ 时间。总的时间复杂度是
$$O(n \log n)$$
代码实现
1 |
|
结果
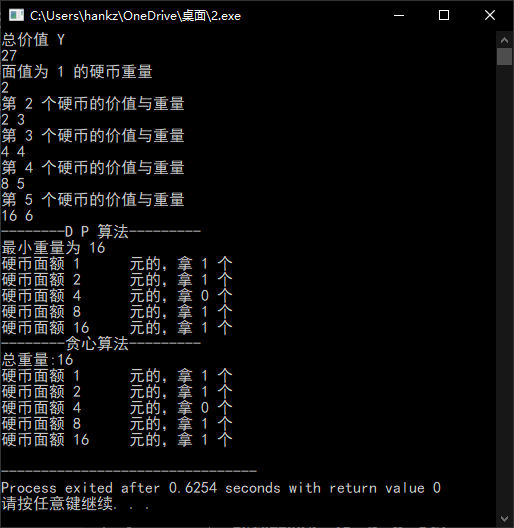
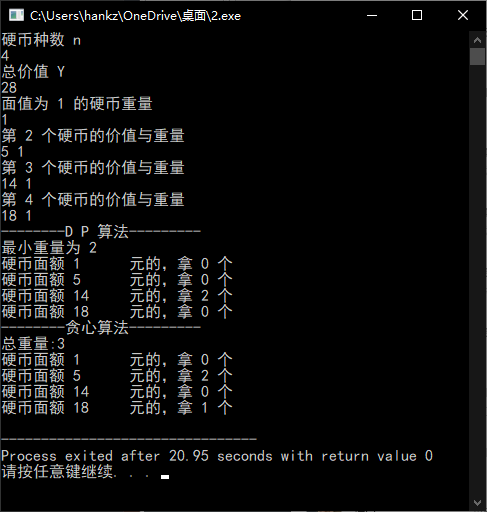
结果不一,为什么?
贪心局限 (看看就好)
我们不妨设这样一串硬币属性:
$$\frac{v_1}{w_1}\le\frac{v_2}{w_2}\le\dots\le\frac{v_n}{w_n}$$
使用前 $k$ 种零钱,总钱数为 $y$。
贪心法的总重为 $G_{k}(y)$,则有如下递推方程
$$\begin{array}{l}
G_{k+1}(y)=w_{k+1}\left\lfloor\frac{y}{v_{k+1}}\right\rfloor+G_{k}\left(y \bmod v_{k+1}\right) \quad k1 \
G_{1}(y)=w_{1}\left\lfloor\frac{y}{v_{1}}\right\rfloor=w_{1} y
\end{array}$$
n=1, 2
$n = 1$ 只有一种零钱,$F_{1}(y) = G_{1}(y) , F_{2}(y) = G_{2}(y)$
$n = 2$, 使用价值大的钱越多($x_{2}$越大),得到的解越好
$F_{2}(y)=\min {0 \leq x{2} \leq\left\lfloor y / v_{2}\right\rfloor}\left{F_{1}\left(y-v_{2} x_{2}\right)+w_{2} x_{2}\right}$
$$\begin{array}{l}
{\left[F_{1}\left(y-v_{2} x_{2}\right)+w_{2} x_{2}\right]} -\left[F_{1}\left(y-v_{2}\left(x_{2}+\delta\right)\right)+w_{2}\left(x_{2}+\delta\right)\right] \
=\left[w_{1}\left(y-v_{2} x_{2}\right)+w_{2} x_{2}\right]-\left[w_{1}\left(y-v_{2} x_{2}-v_{2} \delta\right)+w_{2} x_{2}+w_{2} \delta\right] \
=w_{1} v_{2} \delta-w_{2} \delta=\delta\left(w_{1} v_{2}-w_{2}\right) \geq 0
\end{array}$$
说明$w_{1} ≥ \frac{w_{2}}{v}$,即多使用 $\delta$ 枚第二种硬币的重量更小。
心得体会
贪心算法为什么叫做贪心,是因为其每次都从整个局面出发选看上去对现在最好的选择。但事实告诉我们,这样的选择反而有可能会对局面不利。
DP从子问题出发选对当前子问题最好的选择,符合最优子结构的条件,最终能求出最好的解决。
贪心,真不是好的解决方案呢。
不如着眼现在,做好现在的事情;而不是好高骛远,贪图捷径。
嗯……算法,值得思考,值得发散……
