#实验三  动态规划算法

一．实验目的

掌握动态规划算法的设计与分析步骤以及算法的具体实现。

二．实验要求

实验时间：2学时，对于给定的问题描述，生成实验报告。

三．实验内容

问题描述：给定序列X=<x1,x2, … ,xm>X=<x_{1}, x_{2}, … , x_{m}>, Y=<y1,y2, … ,yn>Y=<y_{1}, y_{2}, … , y{n}> 求 X 和 Y 的最长公共子序列及其长度。

  1. 使用蛮力算法解决问题，给出分析过程。
  2. 使用动态规划算法解决问题，给出分析过程。
  3. 给出算法的具体实现过程（源码及其详细注释）。
  4. 给出算法的运行结果。针对不同的输入，给出两种不同算法时间上的差异。

问题连接-学习通(暂时关闭)

蛮力算法

思路

找出一个串的所有子序列，然后依次与另一个串比较，如果该子序列的排列符合另一个串的排列，则是一个公共子序列。记录子序列的长度，找出最大长度即可。

不难看出，此算法的核心在于找出一个串的所有子序列。
怎么找呢。

我们能够联想到，对于一个物品，选择和不选择，我们都能用0、1来表示。

对于一个序列中的每一个位置，我们也能通过选择与不选择的两种状态。

X串长m。则X有2m2^m个子序列。（因为每个位置可以有两种状态）

我们可以将m转化为二进制，每个位次分别将其与X串的各个位置对应。

复杂度

共有2m2^m个子序列，时间复杂度O(2m)O(2^m)。

每个子序列都需要与Y比较，Y长度为nn，时间复杂度O(n)O(n).
总的时间复杂度O(n2m)O(n2^m).

DP

解决DP问题，最重要的是要找出子问题。所以从这里开始。

子问题

我们假设当前Z=<Z1,Z2, … ,Zk>Z=<Z_{1}, Z_{2}, … , Z_{k}>已经是LCS，可能有xm=ynx_{m} = y_{n}和xm≠ynx_{m} \ne y_{n}：

如果xm = yn

  1. 则zk=xm=ynzk = xm = yn 且 Zk-1是Xm-1和Yn-1的一个LCS.

如果xm != yn

  1. 且有 zk≠xmzk \ne xm，则Z是Xm-1和Y的一个LCS.
  2. 且有zk!=ynzk != yn，则Z是X和Yn-1的一个LCS.

状态转移方程

L[i][j]={0i=0 or j=0max⁡{L[i−1][j],L[i][j−1]}xi≠yj,i>0,j>0L[i−1][j−1]+1xi=yj,i>0,j>0 L[i][j] = \begin{cases} 0 & i = 0 \space or \space j = 0 \\\max\{L[i-1][j],L[i][j-1]\} & x_i\ne y_j,i>0,j>0 \\ L[i-1][j-1]+1 & x_i = y_j,i>0,j>0 \end{cases}

因此，我们只需要从c[0][0]开始填表，填到c[m][n]，所得到的c[m-1][n-1]就是LCS_length.

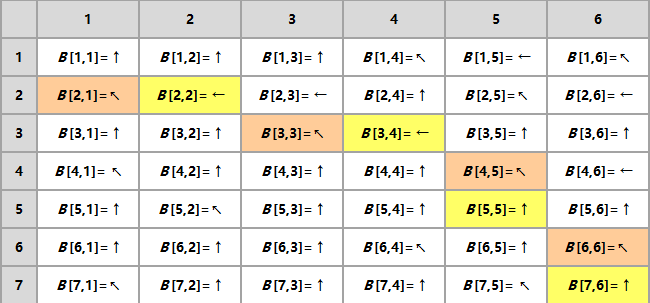
回溯

若想得到LCS，回溯一次b数组，从最后一个位置开始往前遍历：

  1. 如果箭头是↖，则代表这个字符是LCS的一员，存下来后 i-- , j--
  2. 如果箭头是←，则代表这个字符不是LCS的一员，j--
  3. 如果箭头是↑，也代表这个字符不是LCS的一员，i--
  4. 如此直到i=0i = 0或者j=0j = 0时停止，最后存下来的字符就是所有的LCS字符
序列 1 2 3 4 5 6 7
X A B C B D A B
Y B D C A B A \0
Target B C B A
1 2 3 4 5 6
1 B[1,1]= ↑ B[1,2]= ↑ B[1,3]= ↑ B[1,4]=↖ B[1,5]= ← B[1,6]=↖
2 B[2,1]=↖ B[2,2]= ← B[2,3]= ← B[2,4]= ↑ B[2,5]=↖ B[2,6]= ←
3 B[3,1]= ↑ B[3,2]= ↑ B[3,3]=↖ B[3,4]= ← B[3,5]= ↑ B[3,6]= ↑
4 B[4,1]= ↖ B[4,2]= ↑ B[4,3]= ↑ B[4,4]= ↑ B[4,5]=↖ B[4,6]= ←
5 B[5,1]= ↑ B[5,2]=↖ B[5,3]= ↑ B[5,4]= ↑ B[5,5]= ↑ B[5,6]= ↑
6 B[6,1]= ↑ B[6,2]= ↑ B[6,3]= ↑ B[6,4]=↖ B[6,5]= ↑ B[6,6]=↖
7 B[7,1]=↖ B[7,2]= ↑ B[7,3]= ↑ B[7,4]= ↑ B[7,5]= ↖ B[7,6]= ↑

最长公共子序列_DP图

复杂度

该算法无重复地填写了一张(如果需要具体的子序列内容，则是两张)二维表格，每个格子填写时都仅进行了常数次比较。时间复杂度 O(mn)O(mn).

回溯时，在任何情况下，都需要从[m][n]回溯到[1][1]，即回溯时间复杂度为O(m+n)O(m+n).

所以DP算法的时间复杂度为

O(mn)O(mn)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
#include <iostream>
#include <string>
#include <cstring>
#include <ctime>
#include <stack>
#include <cmath>
#define LL long long
using namespace std;

//
void BFLCS(string s1, string s2)
{
    int ans=0;
    int m,n;
    m=s1.length();
    n=s2.length();
    char sub[m],s[m];
    //转化为二进制后，m位需要2^m个数来表示 
    //1代表取，0代表不取。 
    for(int i=1;i<pow(2,m);i++){
        int l=0,j=0,k=0;
        for(j=0;j<m;j++)
        //按位与运算能帮助我们得出哪些字符应该被取，即位为'1' 
        //参考https://blog.csdn.net/boshuzhang/article/details/54021592	 
            if(1&(i>>j))
                sub[l++]=s1[j];
        sub[l]='\0';
        
		j=0;
		//从0开始读子序列 ，直到子序列或者S2串走到末尾 
		//j意味着“是CS”的长度 
        while(j<l && k<n){
            if(sub[j]==s2[k])
                j++;
            k++;
        }
        //如果子序列读完，并且序列长度等于CS长度，意味着整个子序列都是CS 
		//如果这个长度比之前的序列长度都要大。 那么他就是LCS 
        if(j==l && j>ans){
            ans=j;
            strcpy(s,sub);
        }
    }
    printf("LCS长度：%d\n",ans);
    printf("LCS：");
    puts(s);
}
void LCS(string s1,string s2)
{
    int m=s1.length()+1;
    int n=s2.length()+1;
    int **c;
    int **b;
    c=new int* [m];
    b=new int* [m];
    for(int i=0;i<m;i++)
    {
        c[i]=new int [n];
        b[i]=new int [n];
        for(int j=0;j<n;j++)
            b[i][j]=0;
    }
    for(int i=0;i<m;i++)
        c[i][0]=0;
    for(int i=0;i<n;i++)
        c[0][i]=0;
    for(int i=0;i<m-1;i++)
    {
        for(int j=0;j<n-1;j++)
        {
            if(s1[i]==s2[j])
            {
                c[i+1][j+1]=c[i][j]+1;
                b[i+1][j+1]=1;          //1表示箭头为  左上
            }
            else if(c[i][j+1]>=c[i+1][j])
            {
                c[i+1][j+1]=c[i][j+1];
                b[i+1][j+1]=2;          //2表示箭头向  上
            }
            else
            {
                c[i+1][j+1]=c[i+1][j];
                b[i+1][j+1]=3;          //3表示箭头向  左
            }
        }
    }
    cout<<"填表结果："<<endl; 
    for(int i=0;i<m;i++)                //输出c数组
    {
        for(int j=0;j<n;j++)
        {
            cout<<c[i][j]<<' ';
        }
        cout<<endl;
    }
    cout<<"LCS位置："<<endl; 
    stack<char> same;                   //存LCS字符
    stack<int> same1,same2;             //存LCS字符在字符串1和字符串2中对应的下标，方便显示出来
    for(int i = m-1,j = n-1;i >= 0 && j >= 0; )
    {
        if(b[i][j] == 1)
        {
            i--;
            j--;
            same.push(s1[i]);
            same1.push(i);
            same2.push(j);
        }
        else if(b[i][j] == 2)
                i--;
             else
                j--;
    }
    cout<<s1<<endl;                     //输出字符串1
    for(int i=0;i<m && !same1.empty();i++)      //输出字符串1的标记
    {
        if(i==same1.top())
        {
            cout<<'^';
            same1.pop();
        }
        else
            cout<<' ';
    }
    cout<<endl<<s2<<endl;                //输出字符串2
    for(int i=0;i<n && !same2.empty();i++)      //输出字符串2的标记
    {
        if(i==same2.top())
        {
            cout<<'^';
            same2.pop();
        }
        else
            cout<<' ';
    }
    
    cout<<endl<<"LCS长度："<<c[m-1][n-1]<<endl;
    for (int i = 0; i<m; i++)
    {
        delete [] c[i];
        delete [] b[i];
    }
    cout<<"LCS：";
    while(!same.empty())
    {
        cout<<same.top();
        same.pop();
    }
    cout<<endl;
    delete []c;
    delete []b;
}
int main()
{
    string s1="6234572";
    string s2="91822324523452346623452323463";
    int begin,end;
    printf("------------------------\n");
    printf("暴力求解：\n");
    begin=clock(); 
        BFLCS(s1,s2);
    end=clock();
    printf("所用时间：%d毫秒\n",end-begin);
    
    printf("------------------------\n");
    printf("DP求解：\n");
    begin=clock(); 
        LCS(s1,s2);
    end=clock();
    printf("所用时间：%d毫秒\n",end-begin);
    return 0;
}

结果

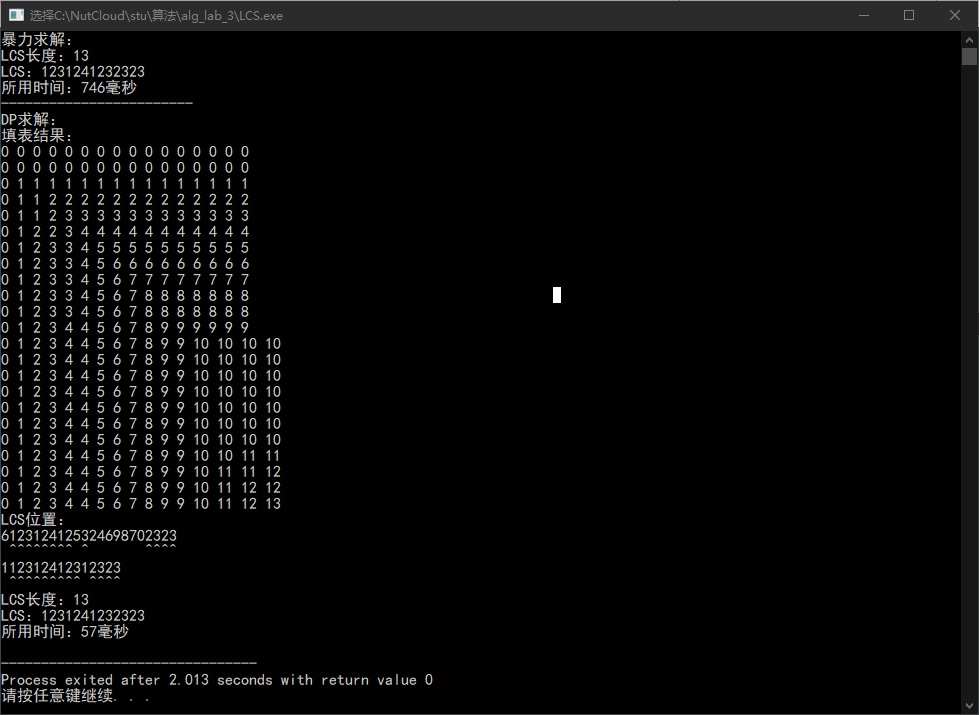
LCS_结果_1
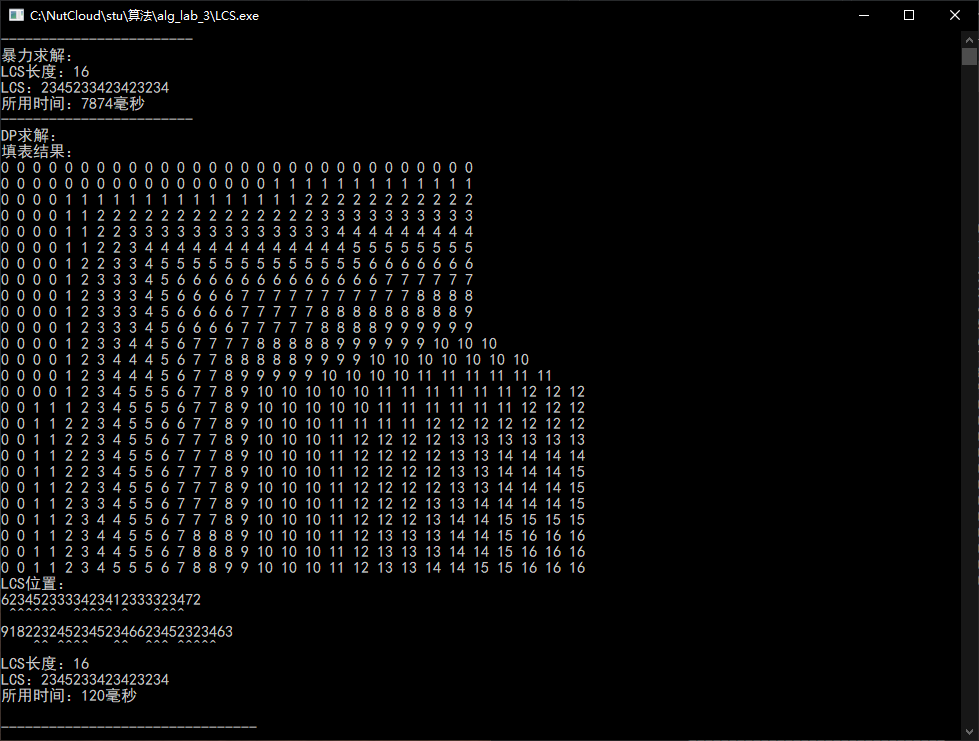
LCS_结果_2
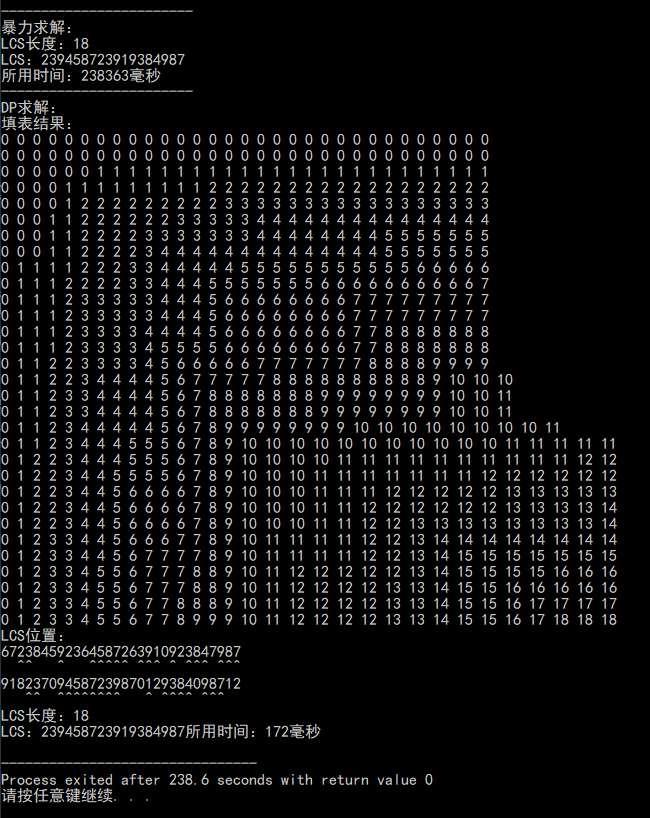
LCS_结果_3

总结

蛮力算法改进

可以看到，蛮力算法的时间复杂度集中在求X，即程序中S1的子序列。若S1足够短，则所消耗的时间会大大降低。

通过比较S1与S2的串长，转而求取较短的串的子序列，可以大幅缩短某些情况下的时间消耗。

S1过长的情况

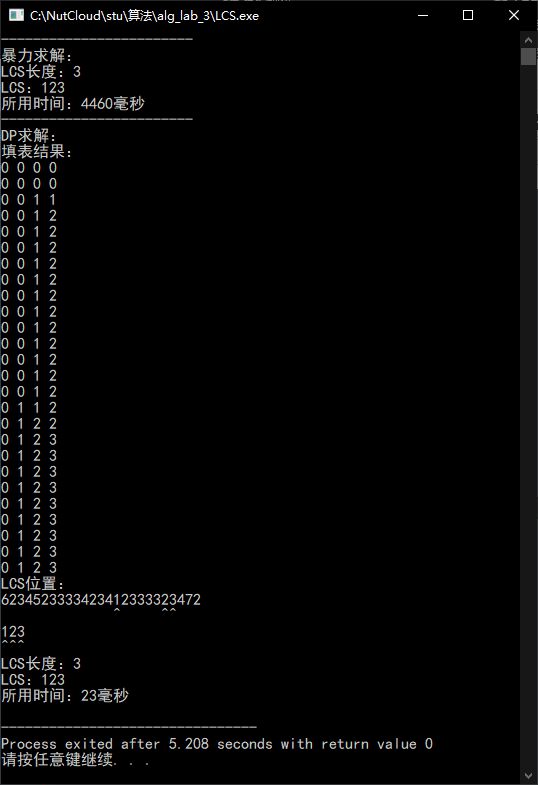
LCS_改进_1

交换S1与S2

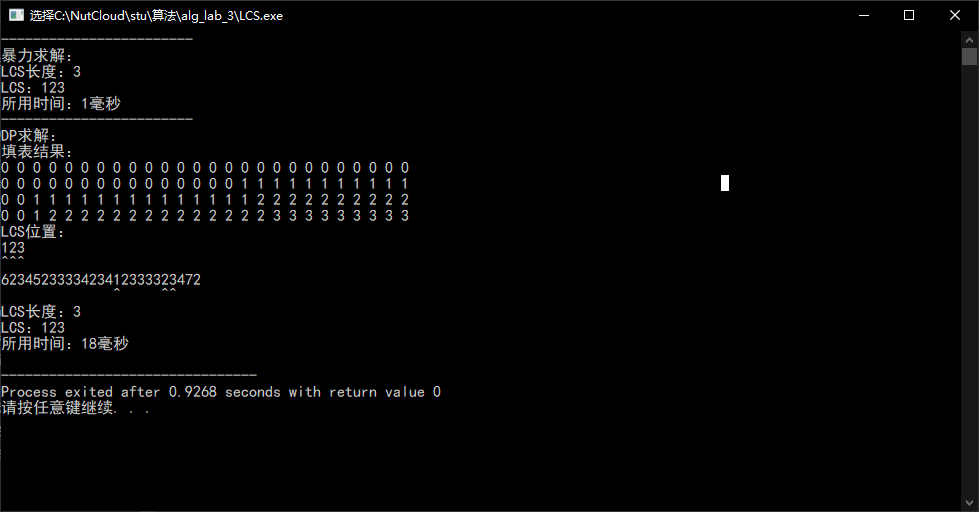
LCS_改进_2

DP改进

对于仅需要求取LCS_length的问题。由于填写第i行时，仅仅需要表格的第i行和第i-1行：利用滚动数组，可以优化空间。同时让更短的串作为列，仅需O(min{m,n})O(min\{m,n\})的空间复杂度。

体会

一般来说，蛮力算法是最容易想到的算法。但在此问题中，对于求出一个串的所有子序列这个问题仍然十分困难。我也是参考了网络上（overview）的方法和同学的建议才想出个所以然。

但要能熟悉了DP的解题思路，明白“找出子问题、构建方程、回溯求解”这三个部分，反而会更加地便于解决问题。